Tangent (geometri)
 For alternative betydninger, se Tangent. (Se også artikler, som begynder med Tangent)
For alternative betydninger, se Tangent. (Se også artikler, som begynder med Tangent)

En tangent til en kurve i et punkt er en ret linje, der approksimerer kurven nær punktet. Hvis kurven er graf for en differentiabel funktion, så er tangentens hældning lig med funktionens differentialkvotient og angiver funktionens væksthastighed i punktet. Tangenten kan godt skære kurven i andre punkter end røringspunktet, men i disse punkter vil den oftest ikke være en tangent. En ret linje kan dermed både være en sekant, og en tangent til en bestemt kurve.
Tangentens ligning
[redigér | rediger kildetekst]En tangent til grafen for en differentiabel funktion har ligning:
hvor f'(x0) udgør differentialkvotienten i punktet.
Tangentplan
[redigér | rediger kildetekst]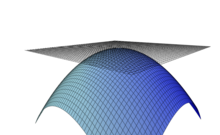
Det er også muligt at finde tangentplanet til en flade. Tangentplanet rører fladen i røringspunktet og dets normalvektor er parallel med fladens normalvektor i punktet. Ligesom tangentlinjen approksimerer planet kurven omkring røringspunktet. For en flade, der kan skrives på formen: er tangentplanet i røringspunktet :
Dette udtryk kan generaliseres til flere dimensioner.
| Spire Denne artikel om geometri er en spire som bør udbygges. Du er velkommen til at hjælpe Wikipedia ved at udvide den. |




