Epoke og ekvinoktium

Inden for astronomi benyttes begreberne epoke og ekvinoktium til at fastlægge tidspunkter til præcis beskrivelse af et himmellegemes position på himlenkuglen.^{: 123 : 18, 73 : 22}

• Ekvinoktium tidsfæster koordinatsystemets beliggenhed i forhold til meget fjerne objekter.
• Epoke tidsfæster himmellegemers beliggenhed i forhold til det valgte koordinatsystem.

Ekvinoktium, der er et tidspunkt, må ikke forveksles med ekvinoktierne, som er en fællesbetegnelse for forårspunktet og efterårspunktet, hvor Solen står ved henholdsvis forårs- og efterårsjævndøgn.

Baggrund

Figuren illustrerer ækvatorsystemet og dets koordinater rektascension og deklination. Den viser et udsnit af himlen, der måler 360° × 100° med himlens ækvator løbende gennem midten (sort ret linje). Desuden vises ekliptika, dvs. Solens årlige bane blandt stjernerne, med orange farve. Et himmellegemes position kan i ækvatorsystemet angives med to sfæriske koordinater, rektascensionen α (alfa) og deklinationen δ (delta). Rektascensionen måles fra forårspunktet, der som her traditionelt markeres med et stiliseret vædderhorn. Det er defineret som det punkt i ekliptika, hvor Solen om foråret krydser himlens ækvator for nordgående. Rektascensionen vokser mod venstre. Værdier er på figuren angivet både i gradmål og i tidsmål. Deklinationen måles vinkelret på ækvator voksende mod himlens nordpol. Position af Solen (gul skive) er markeret tre steder i banen.

Inden for en menneskealder synes stjernernes indbyrdes positioner på himlen at være uforanderlige. Men hvis man sammenligner positioner målt over længere tidsrum (Oldtiden til i dag) eller positioner målt med stor nøjagtighed (den astrometriske rumsonde Gaia), vil man konstatere ændringer Stjernepositioner måles som oftest i det ekvatoreale koordinatsystem (se figur herover) og angives med de to sfæriske koordinater $\alpha$ (rektascension, alfa) og $\delta$ (deklination, delta). De kan sammenlignes med positionsangivelser på jordoverladen, nemlig med geografisk længde $\lambda$ (lambda) og geografisk bredde $\varphi$ (phi). Astronomer angiver traditionelt rektascensionen i tidsmål. Da 360º svarer til 24^h, svarer 15º til 1^h; i denne artikel anvendes dog hovedsageligt gradmål.

Som figuren viser, måles rektascensionen $\alpha$ fra forårspunktet, som er det punkt på himlens ekvator, hvor Solen krydser fra den sydlige til den nordlige himmelhalvkugle; det sker på en af dagene omkring den 21. marts. Deklinationen $\delta$ måles vinkelret på ekvator. Forårspunktets koordinater er derfor $(\alpha$, $\delta )=(0^{\circ },0^{\circ })=(0^{\textrm {h}},0^{\circ })$; efterårspunktets koordinater er $(\alpha ,\delta )=(180^{\circ },0^{\circ })=(12^{\textrm {h}},0^{\circ })$. For himlens nordpol er $\delta =+90^{\circ }$ og for himlens sydpol er $\delta =-90^{\circ }$. Koordinaterne til den polnære stjerne Polaris er $(37^{\circ }57',89^{\circ }16')=(2^{\textrm {h}}32^{\textrm {m}},89^{\circ }16')$.

Årsager til ændring af position

                     Rotation                      Præcession                     Nutation De tider, som indgår i beskrivelsen af de tre fænomener, er meget forskellige: Jordens rotationstid er 23^h 56^m, nutationsperioden er 18.6 år og præcessionsperioden er 25 800 år.

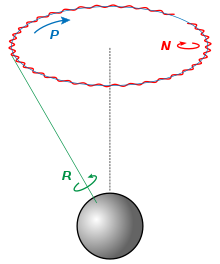
Der er to hovedårsager til, at koordinaterne til et himmellegeme ændres med tiden.

For det første bevæger stjernerne (og Solen) sig rundt om Mælkevejsgalaksens centrum med hver sin hastighed, så set fra os (Solen) optræder en egenbevægelse, som er jo større desto nærmere stjernen er. Den største egenbevægelse findes hos Barnards stjerne, som flytter sig en månediameter på ca. 180 år. Også planeter, kometer og asteroider ændrer deres positioner blandt stjernerne som følge af deres og Jordens bevægelse rundt om Solsystemets tyngdepunkt. Man bruger begrebet "epoke" til at angive positionen til et bestemt tidspunkt.

For det andet ligger ekvatorsystemet ikke fast i rummet. Jordkloden er på grund af sin rotation noget fladtrykt, hvilket bevirker, at gravitationen fra Månen og Solen udøver et kraftmoment på ekvatorudbulingen ("dansehåndtag"). Konsekvensen er, at jordaksen langsomt drejer sig som en snurretop, man taler om præcession, se figuren. Når aksen drejer sig i rummet, så gør ekvatorplanet og dermed himlens ekvator der også, og dette ændrer himmellegemernes koordinater. Man bruger betegnelsen ekvinoktium til at tidsfæste stjernepositioner til et bestemt ekvatorplan.

Hyppigt anvendte epoker og ekvinoktier

Der har gennem tiden været anvendt forskellige standardværdier for disse to tidspunkter. Frem til omkring 1984 anvendte astronomer det "besselske" solår, der var defineret til at begynde på det tidspunkt, hvor Solens middellængde var 280°. Da længden er 270° ved vintersolhverv og Solen flytter sig ca. 1° om dagen, begynder de besselske solår tæt på nytår ifølge den gregorianske kalender. Man betegner det med bogstavet "B", opkaldt efter den tyske astronom Friedrich Bessel. Der gælder for eksempel

• B1900.0 = JDE 2 415 020.3135 = 1899 december 31 19:31
• B1950.0 = JDE 2 433 282.4235 = 1949 december 31 22:10

(Her betegner JDE en fortløbende nummerering af dage, "juliansk dag".)

I 1976 anbefalede Den internationale astronomiske Union, IAU, at man sluttede med at benytte B1950.0 som standardepoke og i stedet fra 1984 og frem gik over til J2000.0^:10 . Man kan forvente, at der snart skiftes til J2050.0 som standardepoke.

I vor tid anvendes juliansk dag (bogstav "J") til angivelse af standardepoker:

• J2000.0 = JDE 2 451 545.00 (eksakt) = 2000 januar 1 kl. 12:00 UT
• J2050.0 = JDE 2 469 807.50 (eksakt) = 2050 januar 1 kl. 00:00 UT
• J2100.0 = JDE 2 488 070.00 (eksakt) = 2100 januar 1 kl. 12:00 UT

Bemærk, at forskellen J2100.0 $-$ J2000.0 er lig med 36525, altså netop antallet af døgn i et århundrede.

Illustration

Tabellen herunder indeholder fire udsnit, A, B, C og D, af himlen omkring forårspunktet, der er skæringspunktet mellem himlens ekvator og ekliptika (orange farve). Forårspunktet markeres traditionelt med et stiliseret vædderhorn. Maskestørrelsen for gradnettet er $10^{\textrm {o}}\times 10^{\textrm {o}}$. De indtegnede himmellegemer er fiktive og skal illustrere koordinatændringer på grund af ændring af epoke og/eller ekvinoktium. De tre blå sekstakkede objekter er kvasarer, der på grund af deres ekstremt store afstande kan anses for ikke at ændre position; de står samme sted på alle fire illustrationer. Desuden er der indtegnet fire stjerner, alle med en fiktivt stor egenbevægelse.

Ekvatorkoordinaterne $(\alpha ,\delta )$ for den røde stjerne øverst til venstre er angivet under hvert panel. I panelerne B og D vises stjernernes oprindelige positioner med grå farve. I panelerne C og D vises gradnettets oprindelige position med grå farve.

• A til B og C til D: Samme ekvinoktium. Koordinatændring som følge af stjernens egenbevægelse gennem 1000 år.
• A til C og B til D: Samme epoke: Koordinatændring som følge af jordaksen præcession gennem 1000 år.
• A til D: Koordinatændring som følge af både egenbevægelse og præcession gennem 1000 år.

Ændring af epoke og ekvinoktium
Fiktivt stjernefelt omkring forårspunktet

A	Epoke: Ekvinoktium:	J2000.0 J2000.0		B	Epoke: Ekvinoktium:	J3000.0 J2000.0
Rød stjerne: $\alpha =22^{\textrm {o}}00',\delta =21^{\textrm {o}}30'$				Rød stjerne: $\alpha =18^{\textrm {o}}00',\delta =16^{\textrm {o}}45'$
C	Epoke: Ekvinoktium:	J2000.0 J3000.0		D	Epoke: Ekvinoktium:	J3000.0 J3000.0
Rød stjerne: $\alpha =36^{\textrm {o}}02',\delta =26^{\textrm {o}}21'$				Rød stjerne: $\alpha =31^{\textrm {o}}39',\delta =21^{\textrm {o}}47'$

Positionsændringer i stjernekataloger

Positioner angivet i et stjernekatalog refererer til et bestemt par af epoke og ekvinoktium, der oftest vil være ens. Som et eksempel på ændringer som følge af en ny standard viser tabellen herunder et uddrag af Bright Star Catalog, der indeholder 9110 stjerner. Nummereringen stammer tilbage fra første udgave fra 1930, der anvendte epoken B1900.0 og var sorteret efter voksende rektascension startende ved 0^h og voksende op mod 24^h. Den nuværende 5. udgave benytter epoke J2000.0, og den mellemliggende præcession har, som det fremgår af tabellen, rundt regnet forøget rektascensioner med 5^m:

Uddrag fra Bright Star Catalog

HR#	Position		Epoke	Egenbevægelse		Mag	Spektrum	*	BD/CD	Rad.hast
	Rektascension	Deklination		Rekt	Dekl
1	00:05:09.90	+45:13:45.00	2000.00	-00.012	-00.018	6.70	A1Vn		BD+44 4550	RV -01
9076	23:59:55.00	-65:34:38.00	2000.00	+00.048	-00.024	4.50	B9IV		CP-66 3819	RV +01
9077	00:00:19.20	-44:17:26.00	2000.00	+00.080	-00.111	6.29	G3IV		CD-4415420	RV +00
9110	00:05:06.20	+61:18:51.00	2000.00	+00.015	+00.005	5.80	B8IVp	*	BD+60 2667	RV +01
En stjerne (*) viser, at der findes yderligere information.

Skift af epoke

For stjerner, hvis position ($\alpha _{0}$, $\delta _{0}$) til epoken $t_{0}$ er kendt og hvis egenbevægelse ($\mu _{\alpha },\mu _{\delta }$) også er bestemt, kan positionen til en anden epoke, $t$, findes ved en simpel lineær beregning:

$\alpha =\alpha _{0}+\mu _{\alpha }\cdot (t-t_{0})$

$\delta =\delta _{0}+\mu _{\delta }\cdot (t-t_{0})$

Eksempel:

For himlens lysstærkeste stjerne, Sirius har man for epoke og ekvinoktium J2000.0 målt følgende koordinater og årlige egenbevægelser:

$\alpha _{2000,2000}=6^{\textrm {h}}45^{\textrm {m}}08.91727^{\textrm {s}}\quad \mu _{\alpha }=-0.54601''/{\textrm {a}}$

$\delta _{2000,2000}=-16^{\textrm {o}}42'58.0171''\quad \mu _{\delta }=-1.22307''/{\textrm {a}}$

I en periode på 50 år ændres koordinaterne derfor med følgende beløb ($15''=1^{\textrm {s}}$):

$\mu _{\alpha }\cdot (t-t_{0})=-0.53601''\cdot 50=-27.3005''=-1.8003^{s}$

$\mu _{\delta }\cdot (t-t_{0})=-1.22307''\cdot 50=-61.1535''=-1'11.1535''$

Koordinaterne til epoken J2050.0 (men stadig til ekvinoktiet J2000.0) bliver derfor

$\alpha _{2050,2000}=6^{\textrm {h}}45^{\textrm {m}}07.117^{\textrm {s}}$

$\delta _{2050,2000}=-16^{\textrm {o}}44'09.17''$

Skift af ekvinoktium

Tilnærmet beregning

For tider, som ikke afviger meget fra standardekvinoktiet (ofte J2000.0) og for stjerner, som ikke ligger tæt ved en af himmelpolerne kan man benytte følgende formler for den årlige ændring af en stjernes position som følge af jordaksens præcession^{: 124 : 239} :

$\Delta \alpha =m+n\cdot \sin(\alpha )\cdot \tan(\delta )$

$\Delta \delta =n\cdot \cos(\alpha )$

hvor $m$ og $n$ er to hjælpestørrelser, som kun ændrer sig langsomt med tiden. De er givet ved

$m=3.07496^{\textrm {s}}+0.00186^{\textrm {s}}\cdot T$

$n=1.33621^{\textrm {s}}-0.00057^{\textrm {s}}\cdot T\quad$ (tidsmål)

$n=20.0431''-00.0085''\cdot T\quad$ (gradmål)

Her betegner $T$ antallet af århundreder forløbet siden standardepoken J2000.0

Eksempel Ovenfor blev positionen af Sirius beregnet for epoken J2050.0 og ekvinoktiet J2000.0. Med de viste formler kan vi finde stjernens koordinater for epoke og ekvinoktium J2050.0. Først det årlige bidrag fra præcessionen:

$T=(2050-2000)/100=0.5$

$m=3.07496^{\textrm {s}}+0.00186^{\textrm {s}}\cdot 0.5=3.07589^{\textrm {s}}$

$n=1.33621^{\textrm {s}}-0.00057^{\textrm {s}}\cdot 0.5=1.335925^{\textrm {s}}\quad$ (tidsmål)

$n=20.0431''-0.0085''\cdot 0.5=20.03885''\quad$ (gradmål)

$\Delta \alpha _{\textrm {p}}=3.07589^{\textrm {s}}+1.335925^{\textrm {s}}\cdot \sin(\alpha )\cdot \tan(\delta )=2.68244^{\textrm {s}}$

$\Delta \delta _{\textrm {p}}=20.03885''\cdot \cos(\alpha )=-3.92213''$

Hertil kommer det årlige bidrag fra egenbevægelsen:

$\Delta \alpha _{\textrm {e}}=-0.53601^{\textrm {s}}$

$\Delta \delta _{\textrm {e}}=-1.22307''$

Efter 50 år er koordinatændringen for Sirius derfor

$\Delta \alpha =50\cdot (\Delta \alpha _{\textrm {p}}+\Delta \alpha _{\textrm {e}})=107.3217^{\textrm {s}}=1^{\textrm {m}}47.3217^{\textrm {s}}$

$\Delta \delta =50\cdot (\Delta \delta _{\textrm {p}}+\Delta \delta _{\textrm {e}})=-257.26''=-6'17.26''$

og koordinaterne dermed

$\alpha _{2050,2050}=\alpha _{2000,2000}+\Delta \alpha =6^{\textrm {h}}46^{\textrm {m}}56.24^{\textrm {s}}$

$\delta _{2050,2050}=\delta _{2000,2000}+\Delta \delta =-16^{\textrm {o}}49'15.28''$

Rigoristisk beregning

Til nøjagtige beregninger og specielt for polnære stjerner anvendes følgende fremgangsmåde: Hvis udgangsepoken er J2000.0, kan følgende fremgangsmåde benyttes^:126 . Man beregner først tre hjælpestørrelser, $\zeta$, $z$ og $\theta$:

$\zeta =2306.2181''\cdot t+0.30188''\cdot t^{2}+0.017988\cdot t^{3}$

$z=2306.2181''\cdot t+1.09468''\cdot t^{2}+0.018203\cdot t^{3}$

$\theta =2004.3109''\cdot t-0.42665''\cdot t^{2}-0.041833\cdot t^{3}$

Her betegner $t$ antallet af julianske århundreder mellem slut- og startekvinoktiet

$t=({\text{JD}}-{\text{JD}}_{0})/36525$

Lad stjernens koordinater ved startekvinoktiet J2000.0 være $\alpha _{0}$ og $\delta _{0}$. Beregn nu størrelserne

$A=\cos(\delta _{0})\cdot \sin(\alpha _{0}+\zeta )$

$B=\cos(\theta )\cdot \cos(\delta _{0})\cdot \cos(\alpha _{0}+\zeta )-\sin(\theta )\cdot \sin(\delta _{0})$

$C=\sin(\theta )\cdot \cos(\delta _{0})\cdot \cos(\alpha _{0}+\zeta )+\cos(\theta )\cdot \sin(\delta _{0})$

Så er koordinaterne $\alpha$ og $\delta$ ved slutekvinoktiet givet ved

$\alpha =\operatorname {arctanxy} \,(B,A)+z$

$\delta =\operatorname {arctanxy} \,({\sqrt {A^{2}+B^{2}}},C)$

Her betegner arctanxy en arcustangens-funktion, som entydigt bestemmer vinklen hørende til et punkt med koordinaterne $(x,y)$.

Eksempel 1

Anvender man de rigoristiske formler på Sirius, finder man

$\alpha _{2050,2050}=6^{\textrm {h}}47^{\textrm {m}}22.123^{\textrm {s}}$

$\delta _{2050,2050}=-16^{\textrm {o}}46'47.506''$

Eksempel 2

Polaris ("Nordstjernen") er en ret lysstærk stjerne, som i de nærmestliggende århundreder står tæt på himlens nordpol. Dens ækvatorkoordinater ændrer sig derfor kraftigt på grund af præcessionen. En efemeride med dens koordinater og en graf, der viser dens position relativt til himlens nordpol, kan ses på dens artikelside.