Fra Wikipedia, den frie encyklopædi
Ved kvadratsætningerne forstår man tre ligninger, som viser sig nyttige ved mange elementære omskrivninger inden for matematisk algebra
[ 1] [ 2] [ 3] [ 4]
De er de følgende tre:
Første kvadratsætning:
(
a
+
b
)
2
=
a
2
+
b
2
+
2
⋅
a
⋅
b
{\displaystyle {\color {Green}(a+b)^{2}}={\color {Red}a^{2}}+{\color {NavyBlue}b^{2}}+{\color {BurntOrange}2\cdot a\cdot b}}
Anden kvadratsætning:
(
a
−
b
)
2
=
a
2
+
b
2
−
2
⋅
a
⋅
b
{\displaystyle {\color {Green}(a-b)^{2}}={\color {Red}a^{2}}+{\color {NavyBlue}b^{2}}-{\color {BurntOrange}2\cdot a\cdot b}}
Tredie kvadratsætning:
(
a
+
b
)
⋅
(
a
−
b
)
=
a
2
−
b
2
{\displaystyle {\color {Green}(a+b)}\cdot {\color {Red}(a-b)}={\color {NavyBlue}a^{2}}-{\color {BurntOrange}b^{2}}}
Størrelserne
a
{\displaystyle a}
b
{\displaystyle b}
herunder .
Sætningerne kan huskes ved hjælp af følgende remser:
”Kvadratet på en sum af to led er lig kvadratet på første led plus kvadratet på andet led plus det dobbelte produkt ”. ”Kvadratet på en differens af to led er lig kvadratet på første led plus kvadratet på andet led minus det dobbelte produkt ”. ”To leds sum ganget med de samme to leds differens er lig med kvadratet på første led minus kvadratet på andet led ”. Sætningerne følger elementært af den generelle regel for udregning af produktet af to flerledede størrelser:
”Hvert led i den ene faktor ganges med hvert led i den anden faktor”. For eksempel er
(
a
+
b
)
⋅
(
c
+
d
+
e
)
=
a
⋅
c
+
a
⋅
d
+
a
⋅
e
+
b
⋅
c
+
b
⋅
d
+
b
⋅
e
{\displaystyle (a+b)\cdot (c+d+e)=a\cdot c+a\cdot d+a\cdot e+b\cdot c+b\cdot d+b\cdot e}
Reglen kan bruges til f. eks. at bevise den tredje kvadratsætning:
(
a
+
b
)
⋅
(
a
−
b
)
=
a
⋅
a
−
a
⋅
b
+
b
⋅
a
−
b
⋅
b
=
a
2
−
b
2
{\displaystyle (a+b)\cdot (a-b)=a\cdot a-a\cdot b+b\cdot a-b\cdot b=a^{2}-b^{2}}
I det tilfælde, at
a
>
b
>
0
{\displaystyle a>b>0}
a
{\displaystyle a}
b
{\displaystyle b}
a
{\displaystyle a}
Af figuren aflæses umiddelbart, at
(
a
+
b
)
2
{\displaystyle (a+b)^{2}}
a
2
{\displaystyle a^{2}}
b
2
{\displaystyle b^{2}}
a
⋅
b
{\displaystyle a\cdot b}
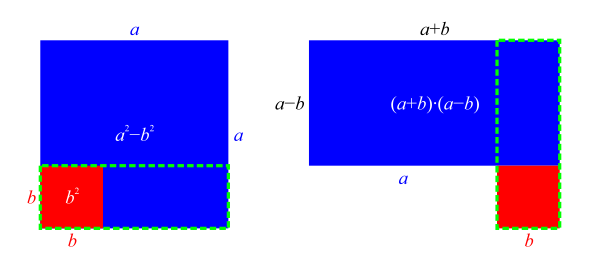
Af figuren aflæses, at
a
2
{\displaystyle a^{2}}
(
a
−
b
)
2
{\displaystyle (a-b)^{2}}
b
2
{\displaystyle b^{2}}
(
a
−
b
)
⋅
b
{\displaystyle (a-b)\cdot b}
a
2
=
(
a
−
b
)
2
+
b
2
+
2
⋅
(
a
−
b
)
⋅
b
=
{\displaystyle a^{2}=(a-b)^{2}+b^{2}+2\cdot (a-b)\cdot b=}
(
a
−
b
)
2
+
b
2
+
2
⋅
a
⋅
b
−
2
⋅
b
2
=
{\displaystyle (a-b)^{2}+b^{2}+2\cdot a\cdot b-2\cdot b^{2}=}
(
a
−
b
)
2
+
2
⋅
a
⋅
b
−
b
2
{\displaystyle (a-b)^{2}+2\cdot a\cdot b-b^{2}}
Af figuren til højre aflæses umiddelbart, at arealet af det blå område er
a
2
−
b
2
{\displaystyle a^{2}-b^{2}}
(
a
+
b
)
⋅
(
a
−
b
)
{\displaystyle (a+b)\cdot (a-b)}
107
2
=
(
100
+
7
)
2
=
100
2
+
7
2
+
2
⋅
100
⋅
7
=
10000
+
49
+
1400
=
11449
{\displaystyle 107^{2}=(100+7)^{2}=100^{2}+7^{2}+2\cdot 100\cdot 7=10000+49+1400=\mathbf {11449} }
55
⋅
45
=
(
50
+
5
)
⋅
(
50
−
5
)
=
50
2
−
5
2
=
2500
−
25
=
2475
{\displaystyle 55\cdot 45=(50+5)\cdot (50-5)=50^{2}-5^{2}=2500-25=\mathbf {2475} }
(
4
⋅
p
−
3
⋅
q
)
2
+
24
⋅
p
⋅
q
=
16
⋅
p
2
+
9
⋅
q
2
−
24
⋅
p
⋅
q
+
24
⋅
p
⋅
q
=
16
⋅
p
2
+
9
⋅
q
2
{\displaystyle (4\cdot p-3\cdot q)^{2}+24\cdot p\cdot q=16\cdot p^{2}+9\cdot q^{2}-24\cdot p\cdot q+24\cdot p\cdot q=\mathbf {16\cdot p^{2}+9\cdot q^{2}} }
x
2
−
y
2
x
+
y
+
x
2
−
y
2
x
−
y
=
(
x
+
y
)
⋅
(
x
−
y
)
x
+
y
+
(
x
+
y
)
⋅
(
x
−
y
)
x
−
y
=
(
x
−
y
)
+
(
x
+
y
)
=
2
⋅
x
{\displaystyle {\frac {x^{2}-y^{2}}{x+y}}+{\frac {x^{2}-y^{2}}{x-y}}={\frac {(x+y)\cdot (x-y)}{x+y}}+{\frac {(x+y)\cdot (x-y)}{x-y}}=(x-y)+(x+y)=\mathbf {2\cdot x} }
Omskrivning af en kvadratisk form for at bestemme den tilhørende kurveform:
x
2
−
2
⋅
x
+
y
2
+
6
⋅
y
−
26
=
0
⇔
{\displaystyle x^{2}-2\cdot x+y^{2}+6\cdot y-26=0\Leftrightarrow }
x
2
−
2
⋅
x
+
1
−
1
+
y
2
+
6
⋅
y
+
9
−
9
−
26
=
0
⇔
{\displaystyle x^{2}-2\cdot x+1-1+y^{2}+6\cdot y+9-9-26=0\Leftrightarrow }
(
x
2
−
2
⋅
x
+
1
)
+
(
y
2
+
6
⋅
y
+
9
)
=
1
+
9
+
26
=
36
⇔
{\displaystyle (x^{2}-2\cdot x+1)+(y^{2}+6\cdot y+9)=1+9+26=36\Leftrightarrow }
(
x
−
1
)
2
+
(
y
+
3
)
2
=
6
2
{\displaystyle \mathbf {(x-1)^{2}+(y+3)^{2}=6^{2}} }
Ligningen fremstiller altså en cirkel med centrum i
(
1
,
−
3
)
{\displaystyle (1,-3)}
6
{\displaystyle 6}
Division med et komplekst tal , her udnyttes, at
i
2
=
−
1
{\displaystyle \mathrm {i} ^{2}=-1}
1
6
+
8
⋅
i
=
6
−
8
⋅
i
(
6
+
8
⋅
i
)
⋅
(
6
−
8
⋅
i
)
=
6
−
8
⋅
i
36
−
(
−
64
)
=
6
−
8
⋅
i
100
=
0.06
−
0.08
⋅
i
{\displaystyle {\frac {1}{6+8\cdot \mathrm {i} }}={\frac {6-8\cdot \mathrm {i} }{(6+8\cdot \mathrm {i} )\cdot (6-8\cdot \mathrm {i} )}}={\frac {6-8\cdot \mathrm {i} }{36-(-64)}}={\frac {6-8\cdot \mathrm {i} }{100}}=\mathbf {0.06-0.08\cdot \mathrm {i} } }
Ved fortsat multiplikation finder man
(
a
+
b
)
3
=
a
3
+
3
⋅
a
2
⋅
b
+
3
⋅
a
⋅
b
2
+
b
3
{\displaystyle (a+b)^{3}=a^{3}+3\cdot a^{2}\cdot b+3\cdot a\cdot b^{2}+b^{3}}
(
a
+
b
)
4
=
a
4
+
4
⋅
a
3
⋅
b
+
6
⋅
a
2
⋅
b
2
+
4
⋅
a
⋅
b
3
+
b
4
{\displaystyle (a+b)^{4}=a^{4}+4\cdot a^{3}\cdot b+6\cdot a^{2}\cdot b^{2}+4\cdot a\cdot b^{3}+b^{4}}
(
a
+
b
)
n
=
a
n
+
(
n
1
)
⋅
a
n
−
1
⋅
b
+
(
n
2
)
⋅
a
n
−
2
⋅
b
2
+
.
.
.
+
(
n
k
)
⋅
a
n
−
k
⋅
b
k
+
.
.
.
+
(
n
n
−
1
)
⋅
a
⋅
b
n
−
1
+
b
n
{\displaystyle (a+b)^{n}=a^{n}+{\tbinom {n}{1}}\cdot a^{n-1}\cdot b+{\tbinom {n}{2}}\cdot a^{n-2}\cdot b^{2}+...+{\tbinom {n}{k}}\cdot a^{n-k}\cdot b^{k}+...+{\tbinom {n}{n-1}}\cdot a\cdot b^{n-1}+b^{n}}
Her er
(
n
k
)
{\displaystyle {\tbinom {n}{k}}}
binomialkoefficient og koefficienterne danner et talskema, som kaldes Pascals trekant .
Kvadratsætningerne omtales ikke som sådan i Kristensen og Rindungs i 1960-erne udbredte lærebogssystem i matematik for gymnasiet; der henvises til anden kvadratsætning som "den velkendte formel"[ 5]
De tre kvadratsætninger behandles i alle nyere lærebøger i matematik for gymnasiet.
Begrebet synes ikke at blive anvendt i udlandet.
Denne side vil blive placeret i følgende kategorier, hvis den bliver flyttet til artikel-navnerummet.
Kategorier :
^ Tommy Boch: Mængder og tal , Forlaget FAG, 1982, side 2.
^ Jens Carstensen, Jesper Frandsen: Matematik 1 for obligatorisk niveau , Systime, 1988, side 27.
^ Jens Carstensen, Jesper Frandsen: Matematik 1 , Systime, 1997, side 14.
^ Knud Erik Nielsen, Esper Fogh: Vejen til matematik AB1 , Forlaget Hax, 2005, side 24 - 25.
^ Erik Kristensen, Ole Rindung: Matematik I , G.E.C.Gads Forlag, 1968, side 34